1.3 谋杀模型

为了侦破谋杀案，我们需要整合更多来自犯罪现场的证据。每一条新证据都将为我们的联合分布添加一个新的随机变量。为了管理这个不断增长的变量数量，我们现在将引入本书的核心概念：概率模型。概率模型包括：

  • 一组随机变量，
  • 这些变量上的一个联合概率分布（即一个为这些变量的每种配置分配一个概率的分布，使得所有可能配置的概率总和为1）。

一旦我们有了概率模型，我们就可以对它包含的变量进行推理，进行预测，了解一些随机变量在给定其他变量值的情况下的值，并且通常可以回答任何可以用模型中包含的随机变量来陈述的可能问题。这使得概率模型成为进行机器学习的极其强大的工具。

我们可以将概率模型视为我们为试图解决的问题所做的一组假设，其中任何涉及不确定性的假设都使用概率来表示。理解这是如何完成的，以及如何使用模型进行推理和预测的最佳方法是查看示例模型。在本章中，我们给出了一个谋杀案的概率模型示例。在后面的章节中，我们将为其他应用构建各种更复杂的模型。本书中所有的机器学习应用都将仅通过使用概率模型来解决。

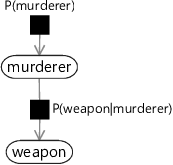
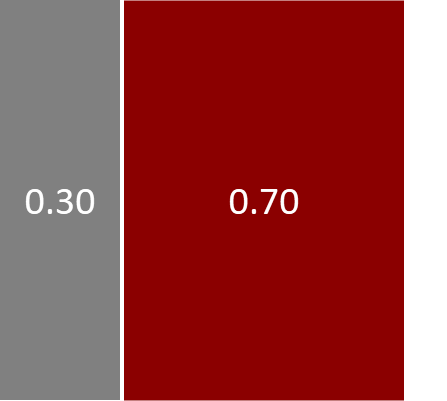
到目前为止，我们已经构建了一个包含两个随机变量的模型：murderer 和 weapon。对于这个双变量模型，我们能够像这样以图形方式写出联合分布：

= ×

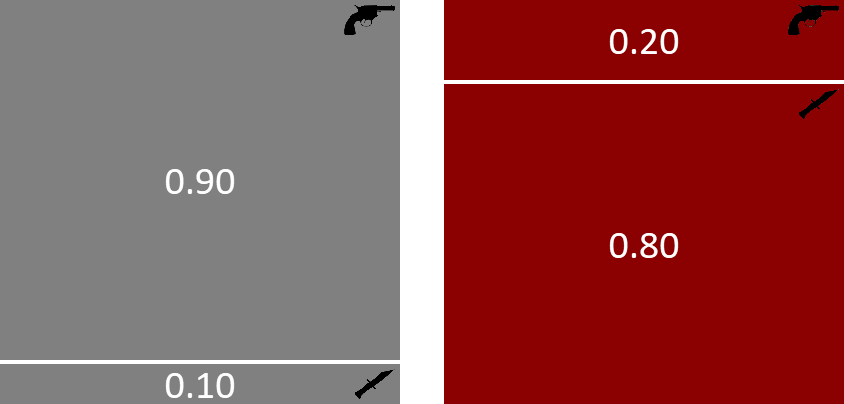
图 1.9：我们的双变量模型的联合分布，显示为两个因子的乘积。

不幸的是，如果我们将模型中的随机变量数量增加到两个（或者可能是三个）以上，我们就无法使用这种图形符号来表示联合分布。但是在真实的模型中，通常会有数百到数亿个随机变量。我们需要一种不同的符号来表示和处理如此大的联合分布。

我们将使用的符号利用了大多数联合分布可以写成多个项或因子的乘积这一事实，每个因子仅涉及少量变量。例如，我们上面的联合分布是两个因子的乘积：P(murderer)P(murderer) 它涉及一个变量，而 P(weapon|murderer)P(weapon|murderer) 它涉及两个变量。即使对于具有数百万变量的联合分布，构成该分布的因子通常也只涉及这些变量中的少数几个。

因此，我们可以使用因子图 [Kschischang et al., 2001] 来表示复杂的联合分布，该图显示了构成该分布的因子以及这些因子所涉及的变量。

图 1.10 显示了上述双变量联合分布的因子图。图中存在两种类型的节点：模型中每个变量对应一个变量节点，联合分布中每个因子对应一个因子节点。变量节点显示为包含变量名称的白色椭圆（或圆角框）。因子节点是小的黑色方块，标有它们所代表的因子。我们将每个因子节点连接到它所涉及的变量节点。例如，因子节点 P(murderer)P(murderer) 仅连接到变量节点 murderer，因为这是它唯一涉及的变量，而 P(weapon|murderer)P(weapon|murderer) 连接到 weapon 和 murderer 变量节点，因为它涉及这两个变量。最后，如果因子定义了其某个变量的分布，我们会在指向该变量（子变量）的边上绘制一个箭头。如果因子定义了一个条件分布，则该因子的其他边连接到作为条件的变量（父变量），并且没有箭头。

Image

图 1.10：谋杀之谜模型的因子图。模型包含两个随机变量 murderer 和 weapon（显示为白色节点），以及两个因子 P(murderer)P(murderer) 和 P(weapon|murderer)P(weapon|murderer)（显示为黑色方块）。

图 1.10 的因子图完整地描述了我们的联合概率，因为可以通过计算由因子节点表示的分布的乘积来找到它。当我们纵观本书中更复杂的因子图时，随机变量（由变量节点表示）上的联合概率分布总是可以写成因子（由因子节点表示）的乘积。 联合分布给出了模型的完整规范，因为它定义了模型中所有随机变量的所有可能值组合的概率。

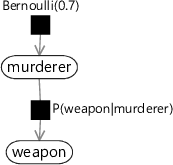
由于我们希望因子图尽可能多地告诉我们关于联合分布的信息，因此我们应该尽可能精确地标记因子。例如，由于我们知道 P(murderer)P(murderer) 定义了 murderer 上的先验分布 Bernoulli(0.7)，因此我们可以将因子标记为“Bernoulli(0.7)”。我们不需要在因子标签中提及 murderer 变量，因为该因子仅连接到 murderer 变量节点，因此分布必须在 murderer 上。这允许对因子图进行更具信息量的标记，如下所示：

Image

图 1.11：谋杀之谜模型的因子图表示，其中明确标记了 murderer 上的伯努利先验。

在本书中，我们的目标是在因子图中标记因子，以便每个因子表示的函数尽可能清晰。

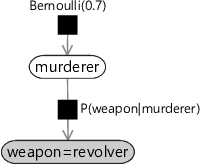
我们还需要介绍因子图表示法的最后一个方面。在我们的双变量模型中进行推断时，我们观察到随机变量 weapon 的值为 revolver。观察随机变量的这一步在基于模型的机器学习中非常重要，因此我们引入了一种特殊的图形表示法来描述它。当观察到随机变量时，因子图中相应的节点会被着色（有时还会标记观察到的值），如图 1.12 所示的我们的谋杀之谜。

Image

图 1.12：谋杀之谜的因子图，其中 weapon 节点已着色，表示已观察到此随机变量，并固定为值 revolver。

使用因子图表示概率模型具有许多优点：

  • 它提供了一种简单的方法来可视化概率模型的结构，并查看哪些变量相互影响。
  • 通过对图进行适当的修改，可以用来激发和设计新的模型。
  • 模型中编码的假设可以清晰地看到并传达给他人。
  • 可以通过对图执行的操作来获得对模型属性的洞察。
  • 可以通过利用因子图结构的有效算法来执行对模型的计算（例如推断）。

我们将在本书中结合具体示例来说明这些要点。

无需计算联合分布的推断

正如我们所观察到的，weapon 的值，我们之前计算了完整的联合分布并用它来评估 murderer 的后验分布。然而，对于大多数现实世界的模型来说，这是不可能做到的，因为联合分布会涉及太多的变量，无法直接计算。相反，既然我们的联合分布表示为因子的乘积，我们可以通过仅使用单个因子来得到相同的结果——这种方式通常计算效率要高得多。关键在于以适当的方式应用概率的乘积和求和规则。根据乘积法则 (1.15)，我们有

$$ P(murderer,weapon)=P(weapon|murderer)P(murderer) (1.22) $$

然而，根据对称性，我们同样可以写出

$$ P(murderer,weapon)=P(murderer|weapon)P(weapon) (1.23) $$

将这两个方程的右边相等并重新排列，我们得到

$$ P(murderer|weapon)=\frac{P(murderer)P(weapon|murderer)}{P(weapon)} (1.24) $$

这是贝叶斯定理或贝叶斯规则 Bayes, 1763] 的一个例子，它在许多[推断计算中起着基础性的作用（参见专栏 1.1）。这里的 P(murderer)P(murderer) 是随机变量 murderer 上的先验概率分布，也是我们在定义谋杀之谜模型时指定的内容之一。类似地，P(weapon|murderer)P(weapon|murderer) 也是我们指定的，称为似然函数，应被视为随机变量 murderer 的函数。左边的量是后验概率分布 P(murderer|weapon)P(murderer|weapon)，它告诉我们，在观察到 weapon 的值之后，我们对 murderer 的了解。

方程 (1.24) 中的分母起着归一化常数的作用，并确保贝叶斯定理的左边正确归一化（即，当对随机变量 murderer 的所有可能状态求和时，总和为 1）。它可以根据先验和似然性使用

$$ P(weapon)=\sum_{murderer} P(weapon|murderer)P(murderer) (1.25) $$

来计算，这源于乘积和求和规则。在使用贝叶斯规则时，有时省略此分母而改写为

$$ P(murderer|weapon) \propto P(weapon|murderer)P(murderer) (1.26) $$

其中 ∝ 表示左边与右边成正比（即，它们在不依赖于 murderer 值的常数范围内相等）。我们不需要计算分母，因为归一化约束告诉我们条件概率分布在 murderer 的所有值上加起来必须为 1。一旦我们评估了 (1.26) 的右边，为 murderer 的两个值分别给出一个数字，我们就可以缩放这两个数字，使它们加起来为 1，从而得到最终的后验分布。

专栏 1.1：贝叶斯定理

贝叶斯定理允许我们用“反向”条件分布来表示诸如 P(A|B)P(A|B) 之类的条件概率分布：

$$ P(A|B)=\frac{P(A)P(B|A)}{P(B)} (1.27) $$

当我们得到由随机变量 B 表示的一些新信息时，贝叶斯定理在我们要更新某个不确定数量 A 的分布时特别有用。例如，在谋杀之谜中，我们想知道凶手 A 的身份，而我们刚刚发现了凶器 B。如果我们不知道 B，那么我们对 A 的了解将由 P(A)P(A) 描述，我们称之为先验。一旦我们知道了 B 的值，我们就可以计算修正后的分布 P(A|B)P(A|B)，称为后验。它们通过反向条件分布 P(B|A)P(B|A) 相关联，后者称为似然。请注意，似然不应被视为 B 上的概率分布，因为假定 B 的值是已知的，而应被视为随机变量 A 的函数，因此也称为似然函数。另请注意，它在 A 上的总和不一定等于 1。

我们也可以用文字来写贝叶斯定理：

$$ posterior=\frac{prior \times likelihood}{normalizer} (1.28) $$

这里的“normalizer”就是 P(B) 的值，是确保后验分布归一化的量。根据求和规则 (1.19)，它由

$$ P(B)=\sum_{A} P(A)P(B|A) (1.29) $$

给出，因此可以从先验和似然函数计算出来。

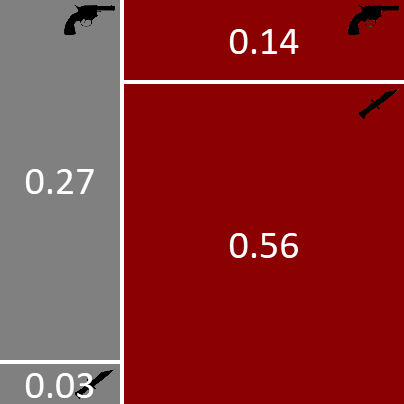
现在让我们将贝叶斯规则应用于谋杀之谜问题。我们知道 weapon=revolver，所以我们可以为 murderer=Grey 和 murderer=Auburn 计算方程 (1.26) 的右边，得到：

$$ P(murderer=Grey|weapon=revolver) \propto 0.3 \times 0.9 = 0.27 $$$$ P(murderer=Auburn|weapon=revolver) \propto 0.7 \times 0.2 = 0.14 $$

这些数字加起来是 0.41。为了得到概率，我们需要将这两个数字缩放以使它们的总和为 1（通过除以 0.41），得到：

$$ P(murderer=Grey|weapon=revolver)=\frac{0.27}{0.41} \approx 0.66 $$$$ P(murderer=Auburn|weapon=revolver)=\frac{0.14}{0.41} \approx 0.34 $$

这和之前的结果一样。虽然我们通过不同的途径得到了相同的结果，但后一种使用贝叶斯定理的方法更可取，因为我们不需要计算联合分布。到目前为止，在我们的谋杀之谜中只有两个随机变量，这看起来可能不是一个显著的改进，但是当我们处理更复杂的问题时，我们会看到概率规则的连续应用使我们能够处理随机变量的小子集——即使在具有数百万变量的模型中也是如此！

本页介绍的概念回顾

  • 概率模型：一组随机变量与一个联合分布相结合，该联合分布为这些变量的每种配置分配一个概率。
  • 因子：通常是少量变量的函数，它们相乘以得到一个联合概率分布（可能涉及大量变量）。因子在因子图中表示为小的黑色方块。
  • 因子图：概率模型的一种表示，它使用一个图，其中包含联合分布中每个因子的因子节点（黑色方块）和模型中每个变量的变量节点（白色，圆形）。边连接每个因子节点到它所引用的变量节点。
  • 变量节点：因子图中的一个节点，表示模型中的一个随机变量，显示为包含变量名称的白色椭圆或圆角框。
  • 因子节点：因子图中的一个节点，表示模型的联合分布中的一个因子，显示为标有因子名称的小黑色方块。
  • 子变量：对于因子节点，箭头指向的连接变量。这表示该因子定义了此变量上的概率分布，可能以连接到此因子的其他变量为条件。因子的子变量通常绘制在该因子的正下方。
  • 父变量：对于因子节点，边上没有指向它们的箭头的连接变量。当因子定义条件概率分布时，这些是作为条件的变量。因子的父变量通常绘制在该因子的上方。
  • 贝叶斯定理：使我们能够在概率模型中进行有效推断的基本定理。它定义了在接收到新信息 B 后如何更新我们对随机变量 A 的信念，以便我们从先验信念 P(A)P(A) 转到给定 B 的后验信念 P(A|B)P(A|B)。有关更多详细信息，请参见专栏 1.1。
  • 似然函数：一个条件概率，被视为其条件变量的函数。例如，当观察到 B 并且我们有兴趣推断 A 时，P(B|A)P(B|A) 可以被视为 A 的函数。重要的是要注意，这不是 A 上的分布，因为 P(B|A)P(B|A) 在 A 的所有值上加起来不必为 1。要从似然函数获得 A 上的分布，您需要应用贝叶斯定理（参见专栏 1.1）。

本页介绍的概念回顾：

  • probabilistic model（概率模型） 一组随机变量与联合分布相结合，为这些变量的每种配置分配一个概率。
  • factors 函数（通常包含少量变量），这些函数相乘得到联合概率分布（可能在大量变量上）。因子在因子图中表示为黑色小方块。
  • factor graph 因子图概率模型的表示形式，它使用一个图形，其中联合分布中的每个因子都有因子节点（黑色方块），模型中的每个变量都有变量节点（白色，四舍五入）。边将每个因子节点连接到它所引用的变量节点。
  • variable node 变量节点因子图中的节点，表示模型中的随机变量，显示为包含变量名称的白色椭圆或圆角框。
  • factor node 因子节点因子图中的节点，表示模型联合分布中的因子，显示为标有因子名称的黑色小方块。
  • child variable 对于 factor 节点，箭头指向的连通变量。这表明该因子定义了该变量的概率分布，可能以与该因子相关的其他变量为条件。因子的子变量通常绘制在该因子的正下方。
  • parent variables 父变量对于因子节点，其边没有箭头指向它们的连通变量。当因子定义条件概率分布时，这些是受条件限制的变量。因子的父变量通常绘制在因子的上方。
  • 贝叶斯定理（Bayes’ theorem） 允许我们在概率模型中进行有效推理的基本定理。它定义了在收到新信息 B 后如何更新我们对随机变量 A 的信念，以便我们从先前的信念 P(A) 转变为给定 B 的后验信念。
  • 似然函数（likelihood function） 被视为其条件变量的函数的条件概率。例如，当观察到 B 并且我们对推断 A 感兴趣时， P(B|A) 可以将其视为 A 的函数。需要注意的是，这不是 A 上的分布，因为 P(B|A) 的 A 的所有值不必求和为 1。要从似然函数获得 A 上的分布，您需要应用贝叶斯定理。

自我评估 1.3

以下练习将有助于巩固您在本节中学到的概念。回顾文本或下面的概念摘要可能会有所帮助。

  1. 使用贝叶斯定理计算 murderer 的后验概率，假设凶器是匕首而不是左轮手枪。将其与您在先前自我评估中的答案进行比较。
  2. 对于您在先前自我评估中选择的场景，绘制与联合分布相对应的因子图。确保尽可能精确地标记因子。验证因子图中的因子乘积等于联合分布。
  3. 使用贝叶斯定理而不是联合分布重复先前自我评估中的推断任务（计算条件变量的后验概率）。检查您是否得到与以前相同的答案。

参考文献

[Kschischang et al., 2001] Kschischang, F. R., Frey, B. J., & Loeliger, H. (2001). Factor graphs and the sum-product algorithm. IEEE Transactions on Information Theory, 47(2):498–519.

[Bayes, 1763] Bayes, T. (1763). An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S. Philosophical Transactions, 53:370–418.

下一节：扩展模型