谋杀之谜

当老都铎王朝豪宅的午夜钟声敲响时，一场狂风暴雨嘎嘎作响地敲响了百叶窗，房子里充满了雷声。布莱克先生的尸体倒在图书馆的地板上，鲜血仍在从致命伤口中渗出。很快赶到现场的是著名的侦探贝叶斯博士，他观察到谋杀时豪宅里只有另外两个人。那么是谁犯下了这种卑鄙的罪行呢？是格雷少校那根正直的柱子吗？还是神秘而诱人的蛇蝎美人奥本小姐？

格雷少校 奥本小姐

图 1.1：谋杀凶手是格雷少校还是奥本小姐？概率让我们能够表达对某个嫌疑人作案的确信程度。

我们将通过调查一起谋杀案来开始研究基于模型的机器学习。虽然这个谋杀之谜看似简单，但它将介绍我们在整本书中将会用到的许多关键概念。你可以使用配套源代码自己重现本章的所有结果。

解决这个谜题的目标是找出凶手的身份。在刚发现尸体时，我们对凶手是奥本小姐还是格雷少校非常不确定。在调查谋杀案的过程中，我们将使用在犯罪现场发现的线索来减少这种不确定性。

我们立即面临的第一个挑战是，我们必须能够处理数值不确定的量。事实上，在我们这个日益由数据驱动的世界中，处理不确定性的需求无处不在。在大多数应用中，我们一开始会处于相当不确定的状态，随着获取更多数据，我们会变得越来越有信心。在谋杀之谜中，我们一开始对凶手是谁非常不确定，然后随着发现更多线索而慢慢变得更加确定。在本书后面，我们会看到更多需要表示不确定性的例子：当两个玩家在 Xbox Live 上对战时，实力更强的玩家更有可能获胜，但这并不是必然的；我们可以相当确定用户会回复某封特定的邮件，但我们永远不能完全确定。

因此，我们需要一个原则性的框架来量化不确定性，这将允许我们以能够表示和处理不确定值的方式创建应用程序和构建解决方案。幸运的是，有一个简单的框架可以用来处理不确定量，它使用概率来量化不确定性的程度。许多人熟悉概率作为特定事件发生频率的概念。例如，我们可能说一枚硬币正面朝上的概率是 50%，这意味着在长期的多次抛掷中，硬币会有大约 50% 的时间正面朝上。在本书中，我们将更普遍地使用概率来量化不确定性，即使是对于只发生一次的情况（如谋杀案）。

表示不确定性

让我们将概率的概念应用到我们的谋杀之谜中。奥本小姐是凶手的概率可以从 0% 到 100%，其中 0% 意味着我们确定奥本小姐是无辜的，而 100% 意味着我们确定她就是凶手。我们也可以用 0 到 1 的标度来表示概率，其中 1 等价于 100%。根据我们对这两个人物的了解，我们可能认为拥有无可挑剔的资历的格雷少校不太可能犯下如此卑劣的罪行，因此我们的怀疑指向神秘的奥本小姐。因此，我们可能假设奥本小姐犯罪的概率是 70%，或者等价地说是 0.7。

为了表达这个假设，我们需要精确地说明这个 70% 的概率指的是什么。我们可以通过用随机变量来表示凶手的身份 —— 这是一个我们不确定其值的变量（一个命名的量）。我们可以定义一个叫做 murderer 的随机变量，它可以取两个值之一：Auburn 或 Grey。给定这个 murderer 的定义，我们可以用下面的形式写出我们的 70% 的假设：

P(murderer = Auburn) = 0.7 (1.1)

其中 P() 表示括号内量的概率。因此等式 (1.1) 可以读作"凶手是奥本小姐的概率是 70%"。我们假设的 70% 可能看起来有点武断 —— 我们现在先用它，但在下一章我们将看到如何从数据中学习这样的概率。

我们知道只有两个潜在的凶手，而且我们还假设只有这两个嫌疑人中的一个实际犯下了谋杀案（换句话说，他们没有一起作案）。基于这个假设，格雷少校犯罪的概率必须是 30%。这是因为这两个概率必须加起来等于 100%，因为两个嫌疑人中必须有一个是凶手。我们可以用同样的形式写出这个概率：

P(murderer = Grey) = 0.3 (1.2)

我们也可以表达这两个概率相加为 1.0 的事实：

P(murderer = Grey) + P(murderer = Auburn) = 1.0 (1.3)

这是概率的归一化约束的一个示例，它指出随机变量的所有可能值的概率之和必须为 1。

如果我们写下随机变量 murderer 的所有可能值的概率，我们会得到：

P(murderer=Grey)=0.3

P(murderer=Auburn)=0.7 (1.4)

写在一起，这是概率分布的一个示例，因为它指定了随机变量 murderer 的每种可能状态的概率。我们使用符号 P(murderer) 来表示随机变量 murderer 的分布。这可以看作是 P(murderer=Auburn) 和 P(murderer=Grey) 的组合的简写表示法。作为使用此表示法的一个例子，我们可以编写归一化约束的一般形式：

$$\sum_{murderer} P(murderer) = 1 (1.5)$$

其中符号 ‘∑’ 表示 ‘sum’，下标 ‘murderer’ 表示和超过随机变量 murderer（即 Auburn 和 Grey）的状态。使用这种表示法，不需要列出随机变量的状态 —— 如果有很多可能的状态，这将非常有用！

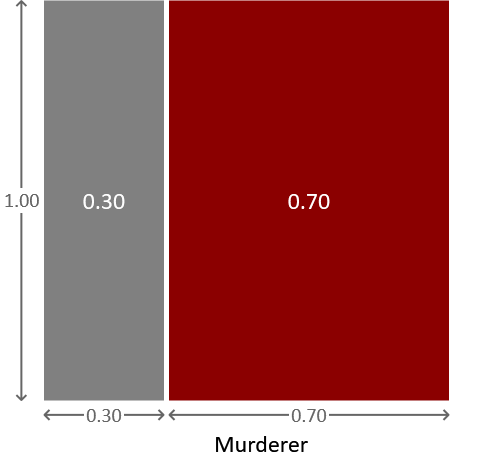
在这一点上，引入概率分布的图形表示是有帮助的，我们可以用它来解释后面的一些计算。图 1.2 显示了一个面积为 1.0 的正方形，它已按两个嫌疑人是凶手的概率成比例划分。

概率区域图

图 1.2：使用面积表示概率。灰色区域表示格雷少校是凶手的概率，红色区域表示奥本小姐是凶手的概率。

由于规范化约束，正方形的总面积为 1.0，并分为两个区域。左侧区域的面积为 0.3，对应于 Major Grey 是凶手的概率，而右侧区域的面积为 0.7，对应于 Auburn 小姐是凶手的概率。因此，该图提供了这些概率的简单可视化。如果我们在正方形中随机选择一个点，那么它降落在与格雷少校对应的区域的概率为 0.3（或相当于 30%），它降落在对应于奥本小姐的区域的概率为 0.7（或相当于 70%）。这种为随机变量选择值的过程，使得选择特定值的概率由特定分布给出，称为抽样。抽样对于理解概率分布或生成合成数据集非常有用——在本书的后面，我们将看到这两个例子。

伯努利分布

这种类型的双状态随机变量的分布在技术上称为伯努利分布，它通常定义在 true 和 false 两种状态上。对于我们的谋杀之谜，我们可以用 true 表示 Auburn，false 表示 Grey。使用这些状态，一个凶手变量上的伯努利分布，其中 true（Auburn）的概率为 0.7，false（Grey）的概率为 0.3，写作 Bernoulli(murderer; 0.7)。更一般地，如果凶手为 true 的概率是某个数 p，我们可以把凶手的分布写作 Bernoulli(murderer; p)。

通常，当我们使用概率分布时，分布适用于哪个变量是明确的。在这种情况下，我们可以简化符号，而不是编写 Bernoulli(murderer;p) ，我们只写 Bernoulli(p)。重要的是要认识到这只是一个速记符号，并不代表 p 的分布。由于我们将在本书中频繁地引用分布，因此使用这种速记方式非常重要，以保持符号清晰简洁。

我们可以使用不同概率值的伯努利分布来表示不同的判断或不确定性评估，从完全无知到完全确定。例如，如果我们完全不知道哪个嫌疑人有罪，我们可以指定 P(murderer) = Bernoulli(murderer; 0.5) 或等价地写作 P(murderer) = Bernoulli(0.5)。在这种情况下，两种状态的概率都是 50%。这是均匀分布的一个例子，其中所有可能的值都是等概率的。在另一个极端，如果我们绝对确定 Auburn 是凶手，那么我们就会设置 P(murderer)=Bernoulli(1) ，或者如果我们确定 Grey 是凶手，那么我们就会 P(murderer)=Bernoulli(0)。这些是点质量的示例，点质量是将所有概率都分配给随机变量的一个值的分布。换句话说，我们确定随机变量的值。

因此，使用这个新术语，我们选择凶手的概率分布为 Bernoulli(0.7)。接下来，我们将展示如何将不同的随机变量关联在一起以开始解决谋杀案。

概念回顾

  • 概率：一种介于 0 和 1 之间的不确定性度量，其中 0 表示不可能，1 表示确定。概率通常以百分比表示（如 0%、50% 和 100%）。

  • 随机变量：一个值不确定的变量（一个命名的量）。

  • 归一化约束：概率分布给出的所有可能值的概率必须相加等于 1。例如，对于 Bernoulli(p) 分布，true 的概率是 p，所以另一个状态 false 的概率必须是 1-p。

  • 概率分布：给出随机变量每个可能值的概率的函数。对于随机变量 A 写作 P(A)。

  • 采样：随机选择一个值，以便选择任何特定值的概率由概率分布给出。这称为从分布中抽样。例如，以下是 Bernoulli(0.7) 分布中的 10 个样本：false, true, false, false, true, true, true, false, true 和 true。如果我们从伯努利 （0.7） 分布中抽取大量样本，那么等于 true 的样本百分比将非常接近 70%。

  • 伯努利分布：双值（二进制）随机变量上的概率分布。伯努利分布有一个参数 p，即值 true 的概率，写为 Bernoulli(p)。例如，Bernoulli(0.5) 代表了公平抛硬币结果的不确定性。

自我评估

以下练习将帮助你巩固在本节中学习的概念：

  1. 为了熟悉思考概率，请估计以下事件的概率，以百分比表示：
    • 用户在访问亚马逊的产品页面后选择购买该产品
    • 用户在收到邮件后选择回复
    • 明天你所在地会下雨
    • 当发生谋杀案时，凶手是受害者家庭成员

根据你的估计，这些事件不发生的概率有多大？（请记住 normalization constraint）。如果可以的话，将您对这些概率的估计与其他人的估计进行比较，并讨论您不同意的地方和原因。

  1. 使用长格式和短格式，将问题 1 的答案写为适当命名的随机变量上的伯努利分布。

  2. 假设我确信你住的地方明天会下雨。什么伯努利分布代表我的信念？如果我确定明天不会下雨，分布会是什么？如果我完全不确定会不会下雨怎么办？

  3. 对于问题 1 中的事件之一，编写一个程序，从伯努利分布中打印出 100 个样本，其中包含事件发生的估计概率（如果您不是程序员，则可以改用电子表格）。要从 Bernoulli(p) 中采样，您首先需要一个介于 0 和 1 之间的随机数（Excel 中的 RAND 或任何编程语言中的随机数函数都可以为您提供）。要获取一个样本，您可以查看随机数是否小于 p - 在这种情况下，样本为 true，否则为 false。有多少比例的样本是真实的？您应该会发现这接近参数 p. 如果增加到 1,000 或 10,000 个样本，您应该会发现该比例越来越接近 p。我们将在本书后面看到为什么会发生这种情况。

下一章：整合证据