贝叶斯博士彻底搜查了整个豪宅。她发现可用的武器只有一把装饰性匕首和一把旧军用左轮手枪。“凶器一定是其中之一”，她得出结论。

到目前为止，我们只考虑了一个随机变量：murderer（凶手）。但现在我们有了关于可能凶器的新信息，我们可以引入一个新的随机变量 weapon（武器）来表示凶器的选择。这个新变量可以取两个值：revolver（左轮手枪）或 dagger（匕首）。有了这个新变量，下一步就是使用概率来表达它与我们现有的 murderer 变量之间的关系。这将让我们能够推理这些变量如何相互影响，并在破案中取得进展。

假设格雷少校是凶手。我们可能认为，他选择左轮手枪而不是匕首作为凶器的概率是 90%，因为他在军队服役期间熟悉这种枪的使用。但如果凶手是奥本小姐，我们可能认为她使用左轮手枪的概率会小得多，比如说 20%，因为她可能不熟悉这种在她出生前就已经停止使用的武器。这意味着随机变量 weapon 的概率分布取决于凶手是格雷少校还是奥本小姐。这被称为条件概率分布，因为其概率值会随另一个随机变量（在本例中是 murderer）而变化。

如果格雷少校是凶手，条件概率选择左轮手枪可以表示为：

P(weapon=revolver | murderer=Grey) = 0.9

在这里，这个方程式左侧的量被读作“鉴于凶手是 Grey，武器是左轮手枪的概率”。它描述了垂直“调节”条左侧数量的概率分布（在本例中为武器的值），该分布取决于条形右侧任何数量的值（在本例中为凶手的值）。我们还说，武器的分配取决于凶手的价值。

由于该武器的唯一其他可能性是匕首，格雷少校选择匕首的概率必须是 10%，因此：

P(weapon=dagger | murderer=Grey) = 0.1

同样，我们也可以用图片的形式表达这些信息，如图 1.3 所示。

图 1.3

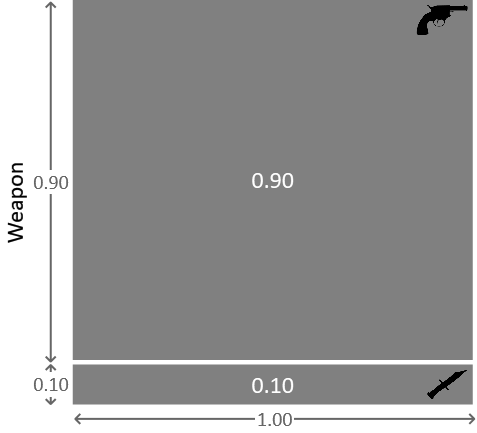
图 1.3：在格雷少校为凶手的条件下，两种武器的概率表示。

在这里，我们看到一个总面积为 1.0 的正方形。上部区域面积为 0.9，对应于武器是左轮手枪的条件概率，而下部区域面积为 0.1，对应于武器是匕首的条件概率。如果我们从正方形内随机均匀地选择一个点（换句话说，从分布中采样），武器是左轮手枪的概率为 90%。

现在假设凶手是奥本小姐。回想一下，我们认为她选择左轮手枪的概率是 20%。因此我们可以写作：

P(weapon=revolver | murderer=Auburn) = 0.2

同样，武器的另一个选择只能是匕首，所以：

P(weapon=dagger | murderer=Auburn) = 0.8

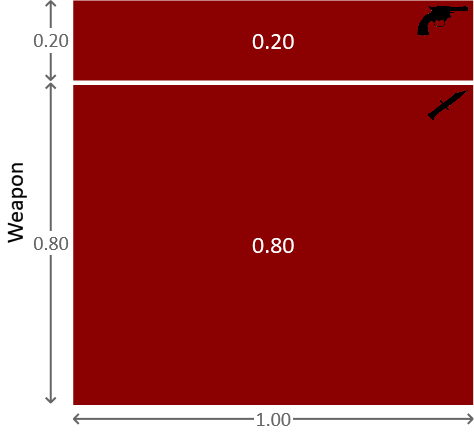
这个条件概率分布可以用图 1.4 所示的方式表示。

图 1.4

图 1.4：在奥本小姐为凶手的条件下，两种武器的概率表示。

我们可以将上述所有信息整合成更紧凑的形式：

P(weapon | murderer=Grey) = [0.9, 0.1]

P(weapon | murderer=Auburn) = [0.2, 0.8]

这可以用更紧凑的形式表示为：

P(weapon | murderer)

和以前一样，我们有一个归一化约束，这是由于对每个嫌疑人来说，使用的武器必须是左轮手枪或匕首。这个约束可以写作：

$$\sum_{weapon} P(weapon | murderer) = 1$$

其中求和是在随机变量 weapon 的两个状态上进行，即 weapon=revolver 和 weapon=dagger，而 murderer 保持在任何固定值（Grey 或 Auburn）。请注意，我们不期望针对 weapon 的列中的概率相加等于 1。这就是为什么紧凑的形式中两个数字加起来不等于 1 的原因。这些概率加起来不需要等于 1，因为它们指的是在两种不同情况下左轮手枪是凶器的概率：如果格雷是凶手，如果奥本是凶手。例如，在两种情况下选择旋转器的概率可能很高，在两种情况下都可能很低，因此归一化约束不适用。

条件概率可以写成条件概率表 （CPT） 的形式——这是我们在本书中经常使用的形式。表 1.1 显示了 P(weapon | murderer) 的条件概率表：

表 1.1

表 1.1：条件概率表。表格列对应于被条件变量 weapon 的值，行对应于条件变量 murderer 的值，表格单元格包含条件概率值。归一化约束意味着任何行中的值必须相加等于 1。我们还在表格中添加了蓝色条来直观地表示概率值。

正如我们刚才讨论的，归一化约束意味着表 1.1 中行的概率必须相加等于 1，但列中的概率不需要相加等于 1。

独立变量

我们已经假设随机变量 murderer 的概率会影响随机变量 weapon 的值。但在某些情况下，我们可能会发现一个变量的概率完全不依赖于另一个变量。例如，如果我们引入一个新的随机变量 raining（下雨）来表示犯罪当天是否下雨，我们可能会认为这与凶手的身份无关。也就是说，在给定 murderer 的情况下 raining 的条件概率与不考虑 murderer 的 raining 的概率完全相同。换句话说，这两个变量是独立的。这种情况在另一个方向上也成立：当日下雨的概率不会因为我们知道凶手是谁而改变。

独立性是基于模型的机器学习中的一个重要概念，因为我们没有明确包含在模型中的任何变量都被假定与模型中的所有变量独立。我们将在本章后面看到更多关于独立性的例子。

让我们花点时间回顾一下我们到目前为止取得的成果。在第一部分中，我们指定了凶手是格雷少校的概率（因此也指定了凶手是奥本小姐的互补概率）。在本节中，我们还写下了每个嫌疑人选择不同武器的概率。在下一节中，我们将看到如何使用所有这些概率来整合犯罪现场的证据并推理凶手的身份。

本页介绍的概念回顾

  • 条件概率分布：一个随机变量 A 的概率分布，其值取决于某个其他变量 B，写作 P(A|B)。例如，如果选择每种凶器（weapon）的概率取决于凶手是谁（murderer），我们可以用条件概率分布 P(weapon|murderer) 来表示这一点。条件概率分布也可以依赖于多个变量，例如 P(A|B,C)。

  • 条件概率表定义条件概率的表，其中列对应于条件变量的值，行对应于条件变量的值。对于条件变量的任何设置，条件变量的概率之和必须为 1，因此任何行中的值之和必须为 1。例如表 1.1 条件概率表，它捕获了给定凶手的武器的条件概率：

  • 自变量如果了解一个随机变量不会提供有关另一个变量的任何信息，则两个随机变量是独立的。从数学上讲，如果

    P(A|B)=P(A)

    P(B|A)=P(B)

    这是基于模型的机器学习中的一个重要概念，因为模型中的所有变量都假定独立于模型之外的任何变量。

自测题 1.1

以下练习将帮助你巩固在本节中学到的概念。可能需要参考正文或下面的概念总结。

  1. 为了熟悉思考条件概率，请为以下每种情况估计条件概率表：

    a. 上班迟到的概率，以交通是否拥堵为条件。

    b. 用户回复电子邮件的概率，以是否认识发件人为条件。

    c. 某一天下雨的概率，以前一天是否下雨为条件。

确保你的条件概率表中的行相加等于1。如果可能的话，将你对这些概率的估计与他人的进行比较，并讨论你们在哪里以及为什么会有分歧。

  1. 从你的生活或工作中选择一个例子，比如上面的例子之一。你应该选择一个二元（两值）变量影响另一个变量的例子。估计表示这两个变量之间影响关系的条件概率表。

  2. 对于问题 1 中的某个事件，编写一个程序，为条件变量的每个值打印出 100 个被条件变量的样本。将样本并排打印，并比较当条件变量为真时与为假时事件发生的样本比例。在每种情况下，事件的频率看起来是否与你的常识一致？如果不一致，回过头来修改你的条件概率表并重试。

下一节：1.2 更新我们的可信部分