贝叶斯博士仔细搜查了图书馆，在书柜里发现了一颗子弹。“嗯，有意思，”她说，“我想这可能是一条重要的线索。”

Image

所以看起来凶器是左轮手枪，而不是匕首。我们的直觉是，这条新证据更强烈地指向格雷少校，而不是奥本小姐，因为格雷少校凭借其年龄和军事背景，比奥本小姐更有可能拥有使用左轮手枪的经验。但我们如何利用这些信息呢？

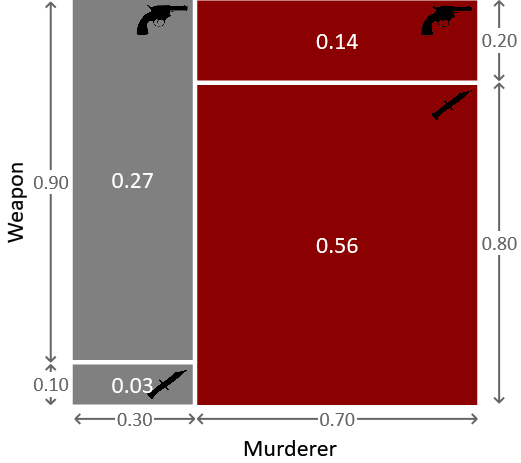
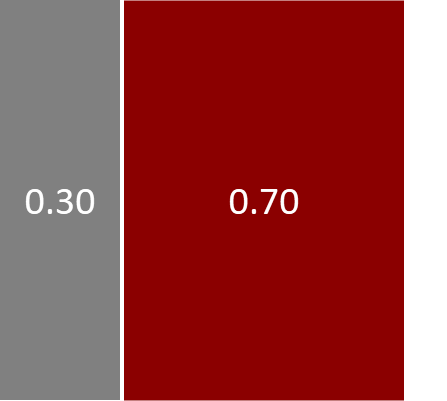
到目前为止，我们所研究的概率可以方便地被认为是描述我们认为谋杀发生过程的一种方式，同时考虑了各种不确定性来源。所以，在这个过程中，我们首先借助图 1.2 来选择凶手。这表明有30%的几率选择格雷少校，70%的几率选择奥本小姐。假设奥本小姐是凶手。然后我们可以参考图 1.4 来选择她使用的武器。她有20%的几率使用左轮手枪，80%的几率使用匕首。让我们考虑奥本小姐选择左轮手枪这一事件。因此，选择奥本小姐和左轮手枪的概率是70% × 20% = 14%。这是选择奥本和左轮手枪的联合概率。如果对其余三种凶手和武器的组合重复此练习，我们会得到两个随机变量的联合概率分布，我们可以如图 1.5 所示进行图形化说明。

Image

图 1.5：凶手和武器这两个随机变量的联合概率表示。

下面的图 1.6 显示了这个联合分布是如何从我们先前定义的分布构建而来的。我们取了正方形中对应于格雷少校的左侧切片，并按照格雷的条件概率方块的两个区域的比例垂直划分了它。同样，我们取了正方形中对应于奥本小姐的右侧切片，并按照奥本的条件概率方块的两个区域的比例垂直划分了它。

= ×

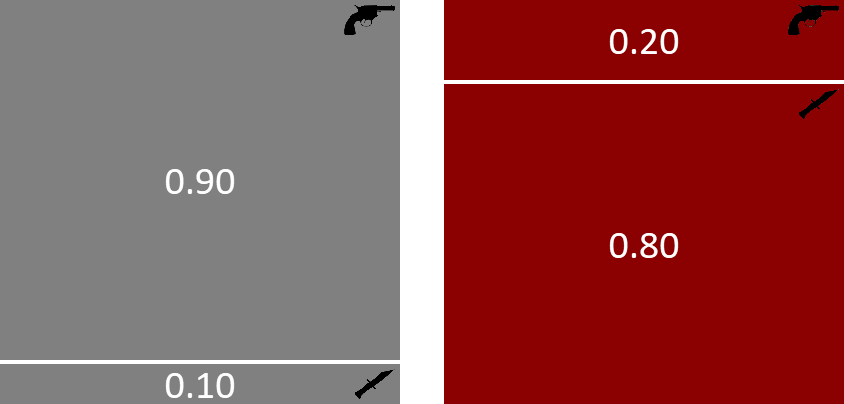
图 1.6：我们的双变量模型的联合分布，表示为两个因子的乘积。

我们将此联合概率分布表示为 P(weapon, murderer)，应读作“武器和凶手的概率”。通常，两个随机变量 A 和 B 的联合分布可以写作 P(A,B)，并指定 A 和 B 每种可能设置组合的概率。因为概率之和必须为1，所以我们有：

$$ \sum_A \sum_B P(A,B) = 1 $$

这里的符号 $ \sum_A $ 表示对随机变量 A 的所有可能状态求和，B 同理。这对应于图 1.5 中正方形的总面积为1，这是因为我们假设世界由一种且仅由一种凶手和武器的组合构成。在这个新正方形中随机选择一个点对应于从联合概率分布中采样。

处理联合概率的两个规则

我们希望利用我们的联合概率分布，根据这条有力的新证据来更新我们对谁是凶手的信念。为此，我们需要引入处理联合分布的两个重要规则。

从上面的讨论中，我们看到我们的联合概率分布是通过取凶手的概率分布乘以武器的条件分布得到的。这可以写成如下形式：

$$ P(\text{murderer, weapon}) = P(\text{murderer}) P(\text{weapon} | \text{murderer}) \quad (1.15) $$

公式 (1.15) 是一个非常重要的结果，称为概率的乘法法则。乘法法则表明，A 和 B 的联合分布可以写成 A 的分布与 B 在 A 值条件下条件分布的乘积，形式如下：

$$ P(A,B) = P(A) P(B|A) \quad (1.16) $$

现在假设我们对图 1.5 中对应格雷少校的左侧两个区域的值求和。它们的总面积是0.3，正如我们预期的那样，因为我们知道格雷是凶手的概率是0.3。这个和是针对武器选择的不同可能性进行的，所以我们可以将其表示为：

$$ P(\text{murderer}=\text{Grey}) = \sum_{\text{weapon}} P(\text{murderer}=\text{Grey, weapon}) \quad (1.17) $$

类似地，第二列中对应凶手是奥本小姐的条目加起来必须是0.7。将这些结合起来，我们可以写成：

$$ P(\text{murderer}) = \sum_{\text{weapon}} P(\text{murderer, weapon}) \quad (1.18) $$

这是概率的加法法则的一个例子，它表明随机变量 A 上的概率分布是通过对 B 的所有值求和联合分布得到的：

$$ P(A) = \sum_B P(A,B) \quad (1.19) $$

在这种情况下，该分布称为 A 的边缘分布，对 B 求和的行为称为边缘化。我们同样可以应用加法法则对凶手进行边缘化，以找出每种武器被使用的概率，而不管是谁使用了它们。如果我们将图 1.5 顶部两个区域的面积相加，我们会看到武器是左轮手枪的概率是 $0.27 + 0.14 = 0.41$，即41%。类似地，如果我们将底部两个区域的面积相加，我们会看到武器是匕首的概率是 $0.03 + 0.56 = 0.59$，即59%。这两个边缘概率加起来是 $0.41 + 0.59 = 1$，这是我们预期的，因为武器要么是左轮手枪，要么是匕首。

加法和乘法法则非常通用。它们不仅适用于 A 和 B 是二元随机变量的情况，也适用于它们是多状态随机变量的情况，甚至当它们是连续的时（此时求和被积分取代）。此外，A 和 B 各自可以代表多个随机变量的集合。例如，如果 $A = (A_1, A_2)$，那么根据乘法法则 (1.16)，我们有：

$$ P(A_1, A_2, B) = P(A_1, A_2) P(B | A_1, A_2) \quad (1.20) $$

类似地，加法法则 (1.19) 给出：

$$ P(A_1) = \sum_{A_2} \sum_B P(A_1, A_2, B) \quad (1.21) $$

最后一个结果特别有用，因为它表明我们可以通过对联合分布中的所有其他随机变量求和来找到特定随机变量的边缘分布，无论有多少其他变量。

乘法法则和加法法则共同提供了我们在整本书中为了操作和计算概率所需的两个关键结果。令人瞩目的是，概率推理丰富而强大的复杂性完全建立在这两条简单的规则之上。

使用联合分布进行推断

我们现在拥有了所需的工具，可以将武器是左轮手枪这一事实纳入考虑。直观上，我们期望这应该会增加格雷是凶手的概率，但要证实这一点，我们需要计算更新后的概率。在我们观察到某些随机变量的值之后，计算修正的概率分布的过程称为概率推断。推断是基于模型的机器学习的基石——它可以用于对情况进行推理、从数据中学习、进行预测——事实上，任何机器学习任务都可以通过推断来实现。

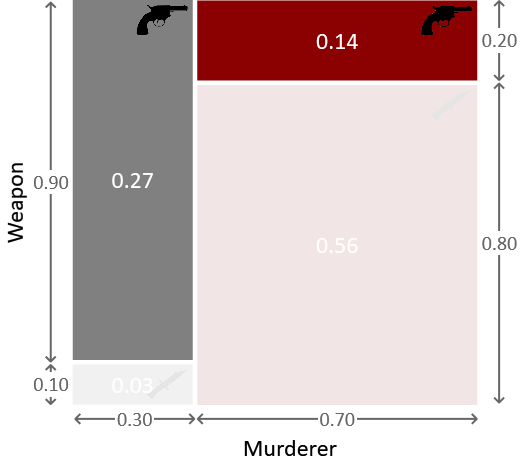
我们可以使用图 1.5 所示的联合概率分布进行推断。在我们观察到用于犯罪的武器之前，这个正方形内的所有点都是等可能的。既然我们知道武器是左轮手枪，我们就可以排除掉对应于武器是匕首的下面两个区域，如图 1.7 所示。

Image

图 1.7：这显示了图 1.5 中的联合分布，其中对应于匕首的区域已被消除。由于剩余两个区域中的所有点都是等可能的，我们看到凶手是格雷少校的概率由左侧灰色框给出的剩余面积的比例给出。换句话说，概率为 $ \frac{0.27}{0.27+0.14} = \frac{0.27}{0.41} \approx 0.66 $，即66%的概率。这明显高于我们在观察到所用武器是左轮手枪之前的30%概率。我们看到我们的直觉因此是正确的，现在看起来格雷更有可能是凶手。在我们看到子弹证据之前分配给格雷是凶手的概率有时称为先验概率（或简称先验），而在看到新证据后修正的概率称为后验概率（或简称后验）。

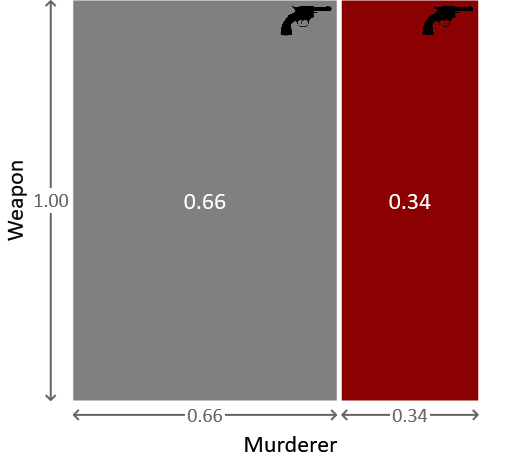
奥本小姐是凶手的概率类似地由 $ \frac{0.14}{0.41} \approx 0.34 $ 给出。因为凶手要么是格雷，要么是奥本，这两个概率加起来再次为1。我们可以通过重新调整图 1.7 中的区域来形象地捕捉这一点，从而得到图 1.8 所示的图表。

Image

图 1.8：在武器是左轮手枪的条件下，格雷或奥本是凶手的后验概率表示。

我们已经看到，随着新数据或证据的收集，我们可以使用乘法和加法规则来修正概率，以反映不确定性水平的变化。该系统可以被视为从这些数据中学习。

Image

那么，经过所有这些努力，我们最终解决谋杀之谜了吗？嗯，从目前的证据来看，格雷似乎更有可能是凶手，但他有罪的概率目前是66%，这感觉太小了，不足以定罪。但我们需要多高的概率呢？为了找到答案，我们求助于威廉·布莱克斯通的原则 [Blackstone, 1765]：

“宁可错放十个有罪之人，也不可错判一个无辜之人。”

因此，我们需要凶手有罪的概率超过 $ \frac{10}{11} \approx 0.91 $，即91%。为了达到这个证明水平，我们需要从犯罪现场收集更多证据，并对我们的联合概率进行相应的扩展，以纳入这些新证据。我们将在下一节中探讨如何做到这一点。

本页介绍的概念回顾：

  • 联合概率 (joint probability)：多个变量的概率分布，给出这些变量共同取特定值组合的概率。例如，P(A,B,C) 是随机变量 A、B 和 C 的联合分布。
  • 概率乘法法则 (product rule of probability)：A 和 B 的联合分布可以写成 A 的分布与 B 在 A 值条件下条件分布的乘积的规则，形式为 $ P(A,B) = P(A)P(B|A) $。
  • 概率加法法则 (sum rule of probability)：随机变量 A 上的概率分布是通过对 B 的所有值求和联合分布得到的规则：$ P(A) = \sum_B P(A,B) $。
  • 边缘分布 (marginal distribution)：通过使用加法法则对联合分布中的所有其他变量求和计算得到的随机变量上的分布。
  • 边缘化 (marginalisation)：对联合分布求和以计算边缘分布的过程。
  • 概率推断 (probabilistic inference)：计算特定随机变量上的概率分布的过程，通常在观察到其他随机变量的值之后。
  • 先验概率 (prior probability)：在看到任何数据之前，随机变量上的概率分布。仔细选择先验分布是模型设计的重要组成部分。
  • 后验概率 (posterior probability)：在考虑了一些数据之后，随机变量上更新的概率分布。推断的目的是计算感兴趣变量的后验概率分布。

自我评估 1.2

以下练习将帮助巩固您在本节中学到的概念。回顾文本或下面的概念摘要可能会有所帮助。

  1. 自行检查图 1.5 中四个区域的联合概率是否正确，并确认它们的总和为1。使用此图计算如果凶器是匕首而不是左轮手枪时，凶手的后验概率。
  2. 选择以下场景之一（接续上一个自我评估）或选择您自己的场景： a. 您是否上班迟到，取决于交通是否拥堵。 b. 用户是否回复邮件，取决于他是否认识发件人。 c. 某一天是否会下雨，取决于前一天是否下雨。 对于您选择的场景，为条件变量选择一个合适的先验概率（例如，交通是否拥堵，用户是否认识发件人，前一天是否下雨）。回顾您在上一个自我评估中估计的条件概率表。使用先验概率和这个条件分布，使用乘法法则计算场景中两个变量的联合分布。像图 1.5 的例子那样，以图形方式绘制这个联合分布。确保标记每个区域的概率值，并且这些值加起来为1。
  3. 现在假设您知道条件变量的值，例如，假设您某天上班迟到了。现在计算条件变量的后验概率，例如，那天交通拥堵的概率。您可以使用上一个问题的图表来实现这一点，方法是划掉不适用的区域，并找到条件事件发生的剩余区域的比例。
  4. 对于您的联合概率分布，编写一个程序打印出两个变量的1000个联合样本。计算具有每种可能值对的样本比例。检查这是否接近您的联合概率表。现在更改程序，使其仅打印出与您上一个问题的已知值一致的样本（例如，您上班迟到的样本）。现在，这些样本中具有每种可能值对的比例是多少？这与您上一个问题的答案相比如何？

参考文献

[Blackstone, 1765] Blackstone, W. (1765). Commentaries on the laws of England.

下一节：谋杀模型