贝叶斯博士掏出她可靠的放大镜，继续在犯罪现场调查。她在布莱克先生尸体附近的地板上，发现了一根落在血泊上的头发。“啊哈！”贝叶斯博士惊呼，“这根头发一定属于谋杀发生时在房间里的人！”她仔细观察这根头发，发现它既不是奥本小姐那一头鲜艳红发的色泽，也不是受害者乌黑的头发，而是格雷少校那种沉稳的银灰色！

Image

现在我们已经掌握了因子图的概念，就可以扩展我们的模型，把这条新增线索纳入考虑。发现头发是一个很强的证据，暗示格雷少校在谋杀发生时出现在现场；但也有另一种可能：头发是奥本小姐偷来的，并被她栽赃到现场，用来误导我们敏锐的侦探。和之前一样，我们可以用条件概率分布把这些想法量化。

用新的随机变量 hair 表示这条线索：如果在现场发现了格雷少校的头发，则 hair=true；否则 hair=false。显然，发现头发比起指向奥本小姐，更强烈地指向格雷少校，但它并不会把奥本小姐完全排除在外。

假设我们认为：如果格雷少校是凶手，他有 50% 的概率会不小心在案发现场留下头发；而如果奥本小姐是凶手，她想到并成功栽赃一根灰色头发的概率只有 5%。那么条件概率分布可以写为：

$$ P(\text{hair}=\text{true}\mid \text{murderer})= \begin{cases} 0.5 & \text{if } \text{murderer}=\text{Grey}\\ 0.05 & \text{if } \text{murderer}=\text{Auburn} \end{cases} \quad (1.32) $$

正如我们之前看到的，这里给出的并不是 hair 上的一个概率分布，而是“在 murderer 取不同值时，hair=true 的条件概率”。因此式 (1.32) 中的两个数不需要相加等于 1。

以这种方式书写条件概率，其实隐含了一个额外假设：在案发现场发现格雷少校的头发，其概率只依赖于谁是凶手，而不依赖于任何其他因素——包括用于作案的武器。之所以会出现这个假设，是因为式 (1.32) 的条件中并没有包含 weapon。用数学语言表达，这个假设是：

$$ P(\text{hair}\mid \text{weapon},\text{murderer})=P(\text{hair}\mid \text{murderer}).\quad (1.33) $$

它表示：一旦我们已经以 murderer 为条件，那么 hair 的分布就与 weapon 的取值无关。这个假设被称为条件独立性（conditional independence）假设。

在考虑一个条件独立性假设时，一个有用的问题是：

“如果我已经知道了条件变量的值，那么再学习到另一个变量的信息，会不会让我对第三个变量有更多了解？”

在这里具体就是：

“如果我已经知道谁是凶手，那么再知道是否发现头发，会不会让我对凶器的选择有更多了解？”

合理地说，答案可能是“会有一点点”（例如，匕首意味着凶手需要更靠近受害者，因此也许更容易掉落头发）。但为了简化，我们假设式 (1.33) 的条件独立性成立。

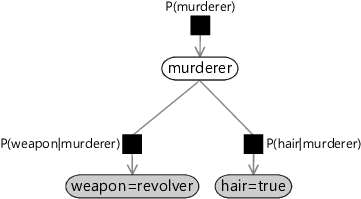
图 1.13 展示了扩展后的模型对应的因子图：它加入了新的变量 hair，以及一个新的因子 $P(\text{hair}\mid\text{murderer})$。条件独立性假设在图上有一个直观的含义：weapon 节点与表示 $P(\text{hair}\mid\text{murderer})$ 的因子节点之间没有边。也就是说，从 weapon 到 hair 的唯一路径必须经过 murderer。

Image

图 1.13：加入新证据后的谋杀之谜因子图。weapon 与 hair 节点被着色，表示它们已被观测（此处为 weapon=revolver、hair=true）。注意 weapon 与因子 $P(\text{hair}\mid\text{murderer})$ 之间缺少直接连接，这对应我们的条件独立性假设。

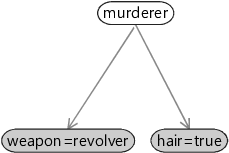
还有一种强调这种独立性假设的图形表示法，叫做贝叶斯网络（Bayesian network，也称 Bayes net）。它会隐藏因子信息，但能提供变量如何（直接或间接）影响彼此的“全局视图”。更多细节见专栏 1.2。

专栏 1.2：贝叶斯网络

Image

如图所示，贝叶斯网络通过隐藏因子来强调“有哪些变量”以及“它们如何相互影响”。在模型设计的早期阶段，当你想先聚焦“要包含哪些变量、哪些变量会影响哪些变量”，而暂时不想深入“影响的具体形式”时，贝叶斯网络会非常有用。

贝叶斯网络的缺点是：它并不能完整刻画一个模型——你还必须在图之外把每一个因子函数写出来，并将两者合起来理解。出于这个原因，本书选择使用因子图，因为它能提供一个更独立、自洽的模型描述。

给定图 1.13 的因子图，我们可以把联合分布写成三个因子的乘积：

$$ P(\text{murderer},\text{weapon},\text{hair})=P(\text{murderer})\,P(\text{weapon}\mid\text{murderer})\,P(\text{hair}\mid\text{murderer}).\quad (1.34) $$

你可以自行检查式 (1.34) 右侧的每一项都对应图 1.13 中的一个因子节点。

增量推断

我们希望在这个新模型中，在给定 weapon 与 hair 的取值后，计算 murderer 的后验分布。由于我们已经在前一个模型中（只引入了 weapon）得到过 P(\text{murderer}\mid\text{weapon})，我们希望把它复用，而不是从头开始。

要在新模型中进行增量推断，我们可以写出贝叶斯定理，但把每一项都以 weapon 为条件：

$$ P(\text{murderer}\mid\text{hair},\text{weapon})= \frac{P(\text{murderer}\mid\text{weapon})\,P(\text{hair}\mid\text{murderer},\text{weapon})}{P(\text{hair}\mid\text{weapon})}. \quad (1.35) $$

和之前一样，我们可以省略分母，把等号替换为比例符号 $\propto$：

$$ P(\text{murderer}\mid\text{weapon},\text{hair}) \propto P(\text{murderer}\mid\text{weapon})\,P(\text{hair}\mid\text{murderer},\text{weapon}). \quad (1.36) $$

由于我们假设在给定 murderer 后，hair 与 weapon 条件独立（式 1.33），因此最后一项可以去掉 weapon：

$$ P(\text{murderer}\mid\text{weapon},\text{hair}) \propto P(\text{murderer}\mid\text{weapon})\,P(\text{hair}\mid\text{murderer}). \quad (1.37) $$

现在我们已知观测到的 weapon 与 hair 的具体取值，可以把观测代入：

$$ P(\text{murderer}\mid\text{weapon}=\text{revolver},\text{hair}=\text{true}) \propto P(\text{murderer}\mid\text{weapon}=\text{revolver})\,P(\text{hair}=\text{true}\mid\text{murderer}). \quad (1.38) $$

接下来我们就可以计算 murderer 的新后验分布。和前面一样，每一项都只依赖于 murderer 的取值，最终再做归一化即可。

把 1.2 节中得到的后验分布（在 weapon=revolver 条件下）代入，并使用式 (1.32) 给出的条件概率，我们得到：

$$ P(\text{murderer}=\text{Grey}\mid\text{weapon}=\text{rev.},\text{hair}=\text{true})\propto 0.66\times 0.50 = 0.33\\ P(\text{murderer}=\text{Auburn}\mid\text{weapon}=\text{rev.},\text{hair}=\text{true})\propto 0.34\times 0.05 = 0.017 $$

这两个数的和是 $0.347$。将它们分别除以该和以归一化后得到：

$$ P(\text{murderer}=\text{Grey}\mid\text{weapon}=\text{rev.},\text{hair}=\text{true})\simeq 0.95\\ P(\text{murderer}=\text{Auburn}\mid\text{weapon}=\text{rev.},\text{hair}=\text{true})\simeq 0.05 $$

综合所有已掌握的证据，格雷少校是凶手的概率现在达到 95%。

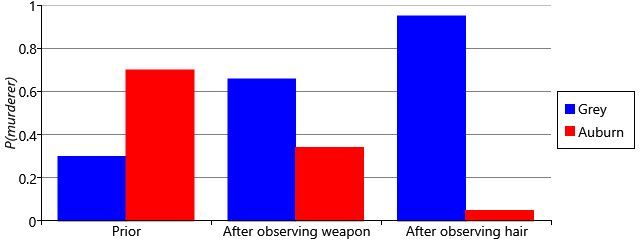
作为回顾，我们可以绘制在整个调查过程中 murderer 的概率分布如何变化（图 1.14）。可以看到，格雷少校作为凶手的概率一开始很低，但随着一条条线索叠加而不断上升。相应地，由于归一化约束以及“二选一”的假设，奥本小姐作为凶手的概率则以相反的方向变化。我们当然可以继续寻找更多证据来让结论更有把握（若证据指向奥本小姐则会反向改变结论），但在本例中我们就到此为止——因为 95% 已经超过了 91% 的定罪门槛。

Image

图 1.14：在谋杀调查过程中 $P(\text{murderer})$ 的演化。

在这一章里，我们构建的谋杀模型包含若干我们“手工设置”的先验与条件概率。但在真实应用中，我们通常并不知道这些概率应当如何设置，而是需要从数据中学习它们。在下一章，我们会看到如何把这些未知概率也表示为随机变量，并用与本章相同的概率推断思想来学习它们。

本页介绍的概念回顾

  • 条件独立性：如果在给定第三个变量 $C$ 的情况下，学习到 $A$ 的信息不会改变我们对 $B$ 的认识（反之亦然），那么称 $A$ 与 $B$ 在给定 $C$ 的条件下条件独立。换句话说，$A$ 的值不直接依赖 $B$，而只通过 $C$ 间接相关。若 $A$ 与 $B$ 在给定 $C$ 后条件独立，则有：
$$ P(A\mid B,C)=P(A\mid C) $$

例如，附近有大型体育赛事（$B$）可能让你预期通勤拥堵（$C$），从而增加你迟到（$A$）的可能性；但如果你已经通过广播知道“并不拥堵”（已知 $C$），那么是否有体育赛事（$B$）就不再影响你对是否迟到（$A$）的判断。

  • 贝叶斯网络：一种图模型，节点对应模型中的变量，边（有向箭头）表示变量之间的直接影响关系。贝叶斯网络不显示因子，但把某个因子的父变量直接用箭头连向子变量。参见本节的专栏 1.2。

自测题 1.4

以下练习将帮助你巩固本节内容。可回顾正文或概念总结。

  1. 延续你在前几节自测题中选择的场景，再选一个会受到“条件变量”影响的额外变量。例如，如果条件变量是“交通很糟糕”，那么受影响变量可以是“我的老板迟到了”。画出包含新变量（以及之前两个变量）的更大模型的因子图，并为新增因子定义一个条件概率表。写下你在设计该模型时做出的条件独立性假设，并用一句话说明理由。
  2. 假设你因子图中的新变量被观测为你选择的某个值（例如“老板迟到”为真）。结合这个新观测与之前自测题中使用的另一个观测（例如“我迟到”为真），推断条件变量（“交通很糟糕”）的后验概率。
  3. 编写一个程序，打印你新模型中三个变量的 1,000 个联合样本。先写下你预期每种三元组出现的频率，然后验证程序输出的频率是否近似符合预期。接着修改程序：只打印同时满足前一题两个观测条件的样本（例如“我迟到”且“老板迟到”）。此时各三元组出现的比例变成了多少？它与上一题的推断结果是否一致？
  4. 再考虑一些可能影响你因子图中三个变量的其他变量。例如，“交通是否糟糕”可能依赖是否下雨，或附近是否有活动发生。在不写条件概率与不定义因子的前提下，画出一个贝叶斯网络，展示这些新变量如何影响现有变量或彼此影响。每条箭头应表达“父变量直接影响子变量”或“父变量（部分）导致子变量”。若可以，向他人展示你的贝叶斯网络并讨论：对方是否理解并同意你选择的变量与条件独立性假设。

下一章：评估人的技能